ERC Consolidator Grant
About Project
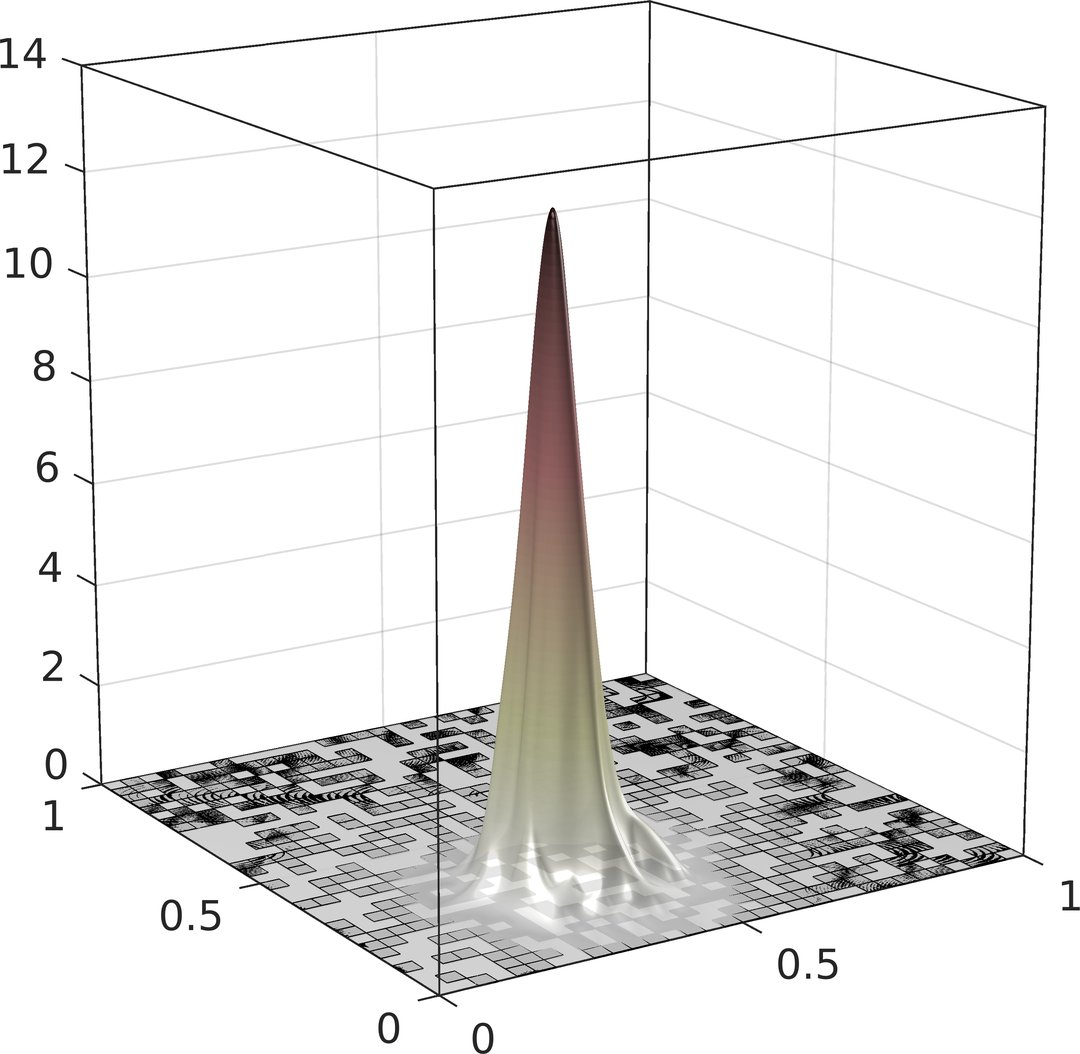
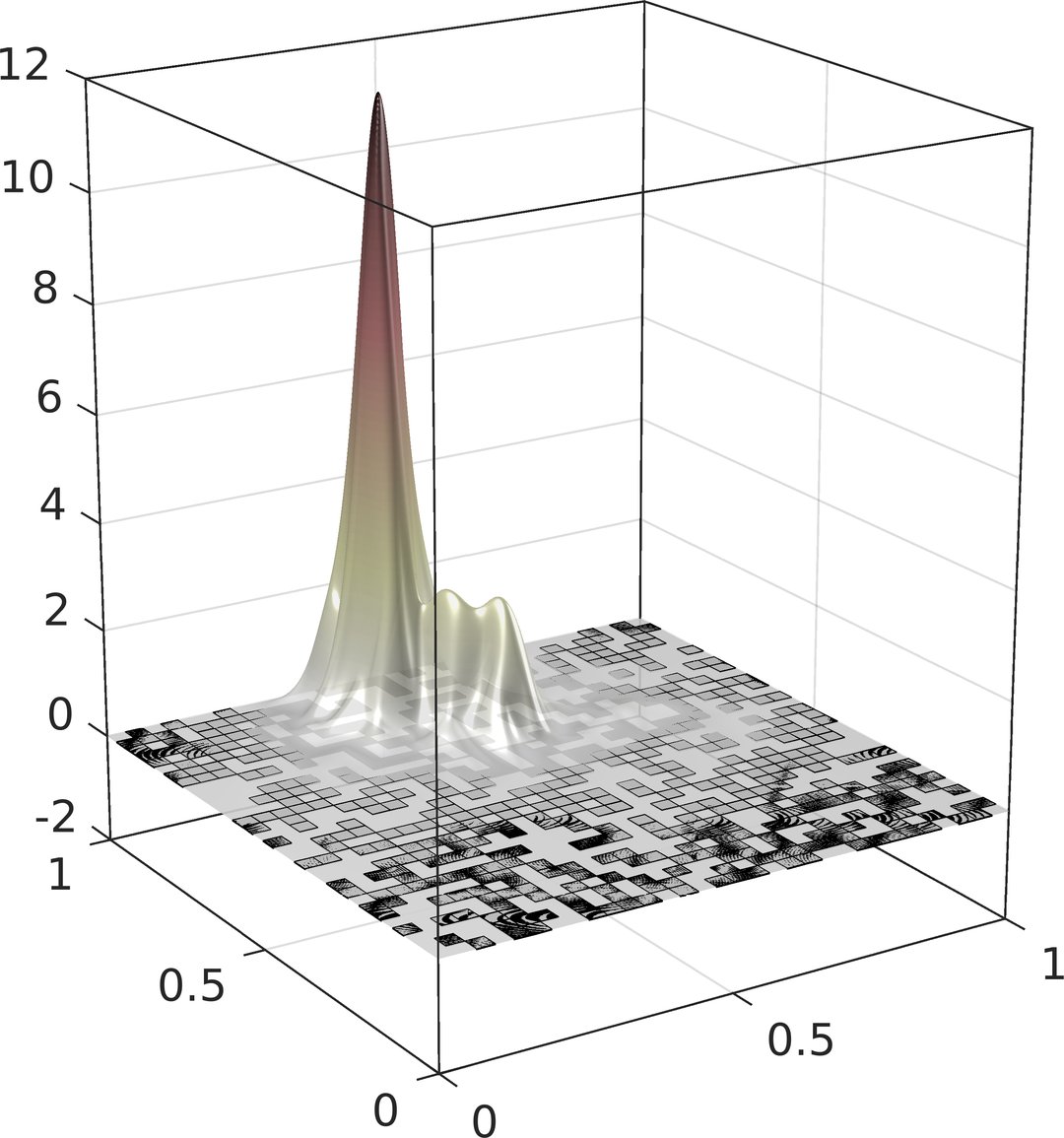
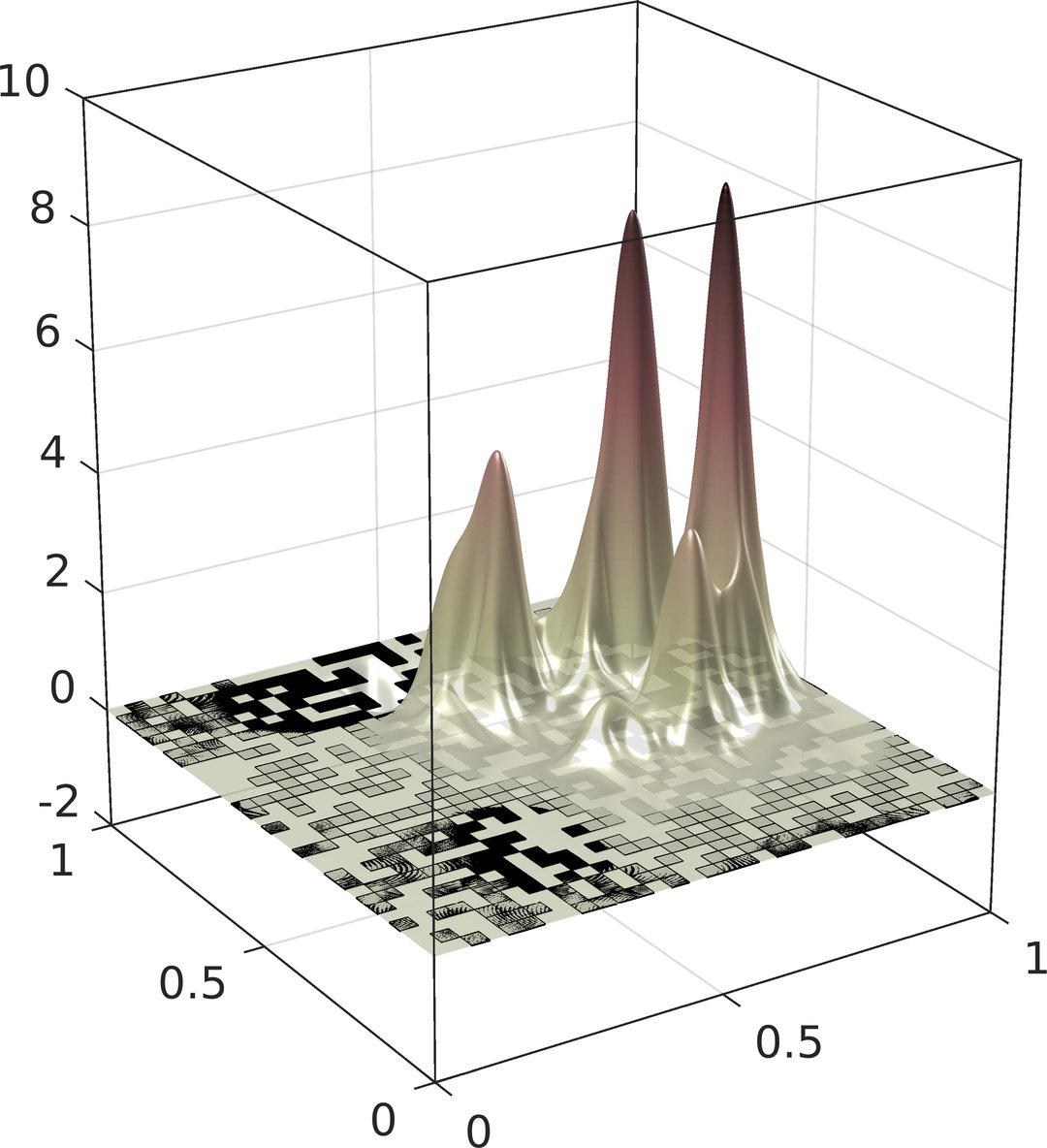

Computational Random Multiscale Problems
PI: Prof. Dr. Daniel Peterseim
Geometrically or statistically heterogeneous microstructures and high physical contrast are the key to astonishing physical phenomena such as invisibility cloaking with metamaterials or the localization of quantum waves in disordered media. Due to the complex experimental observation of such processes, numerical simulation has very high potential for their understanding and control. However, the underlying mathematical models of random partial differential equations are characterized by a complex interplay of effects on many non-separable or even a continuum of characteristic scales. The attempt to resolve them in a direct numerical simulation easily exceeds today's computing resources by multiple orders of magnitude. The simulation of physical phenomena from multiscale models, hence, requires a new generation of computational multiscale methods that accounts for randomness and disorder in a hierarchical and adaptive fashion.
This project concerns the design and numerical analysis of such methods. The main goals are connected to fundamental mathematical and algorithmic challenges at the intersection of multiscale modeling and simulation, uncertainty quantification and computational physics:
(A) Numerical stochastic homogenization beyond stationarity and ergodicity,
(B) Uncertainty quantification in truly high-dimensional parameter space,
(C) Computational multiscale scattering in random heterogeneous media,
(D) Numerical prediction of Anderson localization and quantum phase transitions.
These objectives base upon recent breakthroughs of deterministic numerical homogenization beyond periodicity and scale separation and its deep links to seemingly unrelated theories ranging all the way from domain decomposition to information games and their Bayesian interpretation. It is this surprising nexus of classical and probabilistic numerics that clears the way to the envisioned new computational paradigm for multiscale problems at randomness and disorder.
Community Research and Development Information Service (CORDIS) of the European Commission
Members
- Phone: +49 821 598-3908
Email: jose.garay.fernandez@uni-auni-a.de ()
- Phone: +49 821 598-4816
Email: martin.hermann@uni-auni-a.de ()
- Phone: +49 821 598-3922
Email: hannah.mohr@uni-auni-a.de ()
- Phone: +49 821 598-2194
Email: daniel.peterseim@math.uni-augsburgmath.uni-augsburg.de ()
- Phone: +49 821 598-3931
Email: ngoc1.tran@uni-auni-a.de ()
Events
| Workshop Computational Multiscale Methods, Oberwolfach Research Institute for Mathematics, 27. April - 2. May 2025 |
| GAMM workshop on Numerical Analysis, University of Augsburg, 13.-15. November 2024 |
| Follow-Up Workshop on Multiscale Problems, Hausdorff Research Institute for Mathematics, 19.-23. August 2024 |
| JAM Walkshop on Computational PDEs, Friedrich Schiller University Jena, 30. May - 2. Juni 2024 |
| Workshop on Numerical Analysis of Nonlinear Schrödinger Equations, University of Augsburg, 22. June 2023 |
| Jena-Augsburg-Meeting (JAM) on Numerical Analysis , University of Augsburg, 7.-10. June 2023 |
| One World Numerical Analysis Seminar, online, every two weeks (7. November 2022 - 27. March 2023) |
| Summer School - Uncertainty, Adaptivity, and Machine Learning , University of Augsburg 12.-14. September 2022 |
| Workshop on scattering by random heterogeneous media , University of Augsburg, 13.-15. September 2021 |
Talks
|
[97]
|
D. Peterseim. Riemannian Optimisation Methods for Ground States of Multicomponent Bose–Einstein Condensates, 17. July 2025 at the 15th International Conference on Spectral and High Order Methods (ICOSAHOM), Montreal, Kanada. |
|
[96]
|
D. Peterseim. Quantum Realization of the Finite Element Method, 14. July 2025 at the 15th International Conference on Spectral and High Order Methods (ICOSAHOM), Montreal, Kanada. |
|
[95]
|
J. C. Garay. Spectral Localized Orthogonal Decomposition Methods for Multiscale Elliptic PDEs with High-Contrast Channels, 26. June 2025 at the 29th International Conference on Domain Decomposition Methods (DD29), Politecnico di Milano, Italy. |
|
[94]
|
N. T. Tran. A hybrid high-order method for the biharmonic problem, 24. June 2025 at the 30th Biennial Numerical Analysis Conference, Glasgow, UK. |
|
[93]
|
J. C. Garay. Hierarchical Super-Localized Orthogonal Decomposition for the Solution of Multiscale Elliptic Problems, 17. June 2025 at the 15th Internation Conference on Large-Scale Scientific Computations (LSSC 2025), Sozopol, Bulgaria. |
|
[92]
|
D. Peterseim. Quantum Algorithms for Computational PDEs, 11. June 2025 at the International Conference on Advanced Numerical Schemes for Challenging PDEs, City University of Hong Kong, Hong Kong (plenary talk). |
|
[91]
|
N. T. Tran. A local discontinuous Galerkin method for convex minimization problems, 09. June 2025 at the International Conference on Advanced Numerical Schemes for Challenging PDEs, City University of Hong Kong, Hong Kong. |
|
[90]
|
N. T. Tran. Regularization scheme for the Monge-Ampère equation, 05. June at the Workshop on Recent Advances in Finite Element Methods for Nonlinear PDEs, TianYuan Mathematics Research Center (TYMRC), Kunming, China. |
|
[89]
|
D. Peterseim. Positivity-preserving FEM for the Gross-Pitaevskii eigenvalue problem, 4. June at the Workshop on Recent Advances in Finite Element Methods for Nonlinear PDEs, TianYuan Mathematics Research Center (TYMRC), Kunming, China (invited talk). |
|
[88]
|
D. Peterseim. Quantum Algorithms for Computational PDEs, 29. May 2025 at the Research Seminar at Chinese Academy of Sciences, Beijing, China. (invited talk). |
|
[87]
|
N. T. Tran. A hybrid high-order method for the biharmonic problem, 09. May 2025 at the Austrian Numerical Analysis Day 2025, Salzburg, Austria. |
|
[86]
|
N. T. Tran. Minimal residual discretization of a class of fully nonlinear elliptic PDE, 10. April 2025 at the GAMM Annual Meeting, Poznań, Poland. |
|
[85]
|
M. Hermann. Riemannian Optimisation Methods for Ground States of Multicomponent Bose-Einstein Condensates, 10. April 2025 at the GAMM Annual Meeting, Poznań, Poland. |
|
[84]
|
F. Kröpfl. Deep-Learning-Based Numerical Homogenization of Heterogeneous Media, 9. April 2025 at the GAMM Annual Meeting, Poznań, Poland. |
|
[83]
|
D. Peterseim. Super-Localized Orthogonal Decomposition for High-Frequency Helmholtz Problems, 26. February 2025 at the Conference on Mathematics of Wave Phenomena (WAVES), Karlsruhe, Germany. |
|
[82]
|
D. Peterseim. Computational Relaxation Techniques for Enhanced Damage Modeling, 6. February 2025 at the Workshop Reduced-Order Modeling for Complex Engineering Problems: From Analysis to Practical Implementation, Institute for Mathematical and Statistical Innovation (IMSI), University of Chicago, USA (invited talk). |
|
[81]
|
D. Peterseim. Quantum Algorithms for Computational PDEs, 3. February 2025 at the Research Seminar at EPFL, Lausanne. (invited talk). |
|
[80]
|
N. T. Tran. Hybrid high-order methods for convex minimization problems, 31. January 2025 at the 24th GAMM Seminar on Microstructures, HU Berlin. |
|
[79]
|
D. Peterseim. Localized orthogonal decompositions for high-frequency Helmholtz problems, 21. January 2025 at Advanced Finite Element Methods for Nonlinear PDEs, Tsinghua Sanya International Mathematics Forum (TSIMF), Sanya (invited talk). |
|
[78]
|
D. Peterseim. Nonlinear quantum computing by amplified encodings, 5. December 2024 at Shangahi Jiao Tong University, China (invited talk). |
|
[77]
|
D. Peterseim. Executable Quantum Algorithms for Efficient PDE Simulations, 4. December 2024 at the International Workshop on Scientific Machine Learning, University of Hong Kong, China (invited talk). |
|
[76]
|
N. T. Tran. Minimal residual methods for linear PDE in nondivergence form, 15. November 2024 at the GAMM Workshop on Numerical Analysis, Augsburg. |
|
[75]
|
D. Peterseim. Quantum realization of the finite element method, 2. October 2024 at High-dimensional methods in stochastic and multiscale PDEs, TU Vienna, Austria (invited talk). |
|
[74]
|
D. Peterseim. Quantum realization of the finite element method, 25. September 2024 at The 8th Chinese-German Workshop on Computational and Applied Mathematics, Chengdu, China (invited talk). |
|
[73]
|
N. T. Tran. Hybrid high-order methods for convex minimization problems, 24. September 2024 at The 8th Chinese-German Workshop on Computational and Applied Mathematics, Chengdu, China. |
|
[72]
|
N. T. Tran. Discrete weak duality of hybrid high-order methods for convex minimization problems, 11. September 2024 at Chemnitz Finite Element Symposium 2024, TU Chemnitz. |
|
[71]
|
D. Peterseim. Super-localized Numerical Homogenization, 17. July 2024, Academy of Mathematical and System Sciences, Chinese Academy of Sciences, Beijing, China (invited talk). |
|
[70]
|
J. C. Garay. Hierarchical Super-Localized Orthogonal Decomposition Methods for Multi-Scale Elliptic Problems, 17. July 2024 at the International Conference on Scientific Computation and Differential Equations (SciCADE 2024), National University of Singapore, Singapore. |
|
[69]
|
D. Peterseim. Quantum Realization of the Finite Element Method. 21. June 2024 at the European Finite Element Fair, University College London. |
|
[68]
|
N. T. Tran. Guaranteed lower eigenvalue bounds with hybrid high-order methods, 13. June 2024 at the 10th International Conference on Computational Methods in Applied Mathematics (CMAM-10), Bonn. |
|
[67]
|
J. C. Garay. Hierarchical Super-Localized Orthogonal Decomposition Methods for the Solution of Multi-Scale Elliptic Problems, 10. June 2024 at the 10th International Conference on Computational Methods in Applied Mathematics (CMAM-10), Bonn. |
|
[66]
|
N. T. Tran. Finite element methods for linear PDE of second order in nondivergence form, 31. May 2024 at the JAM Walkshop on Computational PDEs, Jena. |
|
[65]
|
D. Peterseim. Quantum Solver for Partial Differential Equations, 22. April 2024 at the Modern Methods for Differential Equations of Quantum Mechanics workshop, Banff International Research Station (BIRS), Banff. |
|
[64]
|
N. T. Tran. Regularization scheme for the Monge-Ampère equation in 2d, 4. March 2024 at Advanced Finite Element Methods for Nonlinear PDEs, Tsinghua Sanya International Mathematics Forum (TSIMF), Sanya (invited talk). |
|
[63]
|
J. C. Garay. Multiscale finite element methods for an elliptic optimal control problem with rough coefficients and control contraints, 31. January 2024 at the 28th International Conference on Domain Decomposition Methods (DD28), King Abdullah University of Science and Technology (KAUST), Thuwal (invited talk). |
|
[62]
|
D. Peterseim. Superlocalized wave function approximation for the Gross-Pitaevskii equation, 5. December 2023 at the International Workshop an Multiscale Model Reduction and Scientific Machine Learning, Chinese University of Hong Kong (invited talk). |
|
[61]
|
D. Peterseim. Homogenization and computational methods, 28. November 2023 at the workshop on new trends in homogenization, Roscoff, France (invited talk). |
|
[60]
|
D. Peterseim. Computational polyconvexification of isotropic functions, 23. September 2023 at the 11th Workshop on Numerical Methods for Evolution Equations, FORTH Heraklion, Crete (invited talk). |
|
[59]
|
D. Peterseim. Consolidator grant “Computational Random Multiscale Problems”, 19. September 2023 at the EMS & ECMI Zoom Panel on ERC Mathematics (invited talk, online). |
|
[58]
|
D. Peterseim. Numerical Simulation of Nonlinear Eigenvector Problems, 6. September 2023 at the European Conference on Numerical Mathematics and Advanced Applications (ENUMATH), Lisbon (plenary talk). |
|
[57]
|
H. Mohr. Super-localized numerical stochastic homogenization, 4. September 2023 at the European Conference on Numerical Mathematics and Advanced Applications (ENUMATH), Lisbon. |
|
[56]
|
J. C. Garay. DD-LOD: A Localized Orthogonal Decomposition Method for Elliptic Problems with Rough Coefficients Based on Domain Decomposition Techniques, 10. July 2023 at the Mathematics of Computation Research Seminar, Universität Bonn. |
|
[55]
|
J. C. Garay. Multiscale Finite Element methods fo an Elliptic Optimal Control Promblem with Rough Coefficients and Control Constraints, 29. June 2023 at the 29th Biennial Numerical Analysis Conference, University of Strathclyde, Glasgow. |
|
[54]
|
D. Peterseim. Multiscale methods for operator compression and surrogate learning, 28. June 2023 at the 29th Biennial Numerical Analysis Conference, University of Strathclyde, Glasgow (invited talk, plenary talk). |
|
[53]
|
M. Hauck. Super-localized numerical homogenization, 28. June 2023 at the 29th Biennial Numerical Analysis Conference, University of Strathclyde, Glasgow. |
|
[52]
|
D. Peterseim. Multiresolution Super-Localized Orthogonal Decomposition, 14. June 2023 at the Foundations of Computational Mathematics (FoCM), Paris (invited talk). |
|
[51]
|
D. Peterseim. Numerical simulation of nonlinear Schrödinger equations, 17. April 2023 at the Computational methods for multiple scattering workshop, Isaac Newton Institute for Mathematical Sciences, Cambridge (invited talk). |
|
[50]
|
M. Hauck. Super-localized numerical homogenization: Applications and recent advances, 21. March 2023 at the Finite Element Workshop, Universität Jena. |
|
[49]
|
D. Peterseim. Polyconvexifcation of isotropic functions, 20. March 2023 at the Finite Element Workshop, Universität Jena (invited talk). |
|
[48]
|
D. Peterseim. ERC Grant Application - Personal Experience, 1. March 2023 at the SIAM Conference on Computational Science and Engineering, Amsterdam (invited talk). |
|
[47]
|
D. Peterseim. Super-localized numerical homogenization, 8. February 2023 at the Numerical Analysis Seminar, University of Hong Kong (invited talk, online). |
|
[46]
|
D. Peterseim. On the localization problem in numerical deterministic and stochastic homogenization, 28. January 2023 at the 22nd GAMM Seminar on Microstructures, TU Wien (invited talk). |
|
[45]
|
D. Peterseim. On the localization problem in numerical deterministic and stochastic homogenization, 25. January 2023 at the Applied and Computational Mathematics seminars, University of Edinburgh (invited talk). |
|
[44]
|
M. Hauck. A reduced basis super-localized orthogonal decomposition, 19. January 2023 at the Research Seminar Numerical Analysis, Universität Jena. |
|
[43]
|
P. Freese. Numerical homogenization of dispersive Maxwell systems, 12. December 2022 at Kolloquium für Angewandte Mathematik, Technische Universität Hamburg (invited talk). |
|
[42]
|
D. Peterseim. Nonlinear eigenvector problems and the simulation of Bose-Einstein condensates, 8. December 2022 at Lothar-Collatz-Kolloquium für Angewandte Mathematik, Universität Hamburg. |
|
[41]
|
P. Freese. A super-localized generalized finite element method, 1. December 2022 at the Research Seminar Numerical Analysis, Universität Jena. |
|
[40]
|
D. Peterseim. Nonlinear eigenvector problems and the simulation of Bose-Einstein condensates, 17. November 2022 at the Research Seminar Numerical Analysis, Universität Jena (invited talk). |
|
[39]
|
M. Hauck. Super-localization of elliptic multiscale problems with an extension to spatial networks, 28. September 2022 at Computational and Applied Mathematics (CAM) seminar, Chalmers University of Technology and University of Gothenburg. |
|
[38]
|
P. Freese. Super-localized orthogonal decomposition for high-frequency Helmholtz problems, 30. August 2022 at CMAM, Vienna, Austria. |
|
[37]
|
F. Bonizzoni. A greedy method for the tracking of eigensolutions to parametric PDEs, 30. August 2022 at the CMAM 2022, Vienna, Austria. |
|
[36] |
P. Freese. Super-localization for convection-dominated diffusion problems, 28. July 2022 at SciCADE, Reykjavik. |
|
[35]
|
M. Hauck. Super-localization of the elliptic multiscale problem, 28. July 2022 at the 27th International Domain Decomposition Conference, Prague. |
|
[34]
|
F. Bonizzoni. Rational-based MOR methods for Helmholtz frequency response problems with adaptive finite element snapshots, 25. July 2022 at the 15th International Conference on Mathematical and Numerical Aspects of Wave Propagation (WAVES), ENSTA Paris in Palaiseau, France. |
|
[33]
|
P. Freese. Super-localized orthogonal decomposition for convection-dominated diffusion problems, 14. July 2022 at EQUADIFF, Brno. |
|
[32]
|
D. Peterseim. Nonlinear Eigenvector problems and the simulation of Bose-Einstein condensates, 14. July 2022 at EQUADIFF, Brno (invited talk). |
|
[31]
|
P. Freese. Super-localized orthogonal decomposition for convection-dominated diffusion problems, 6. July 2022 at Workshop on Numerical Methods and Analysis in CFD, Weierstrass Institute, Berlin. |
|
[30]
|
F. Bonizzoni. BGG sequences of tensor product finite elements with arbitrary continuity, 22. June 2022 at the Workshop “Hilbert Complexes: Analysis, Applications, and Discretizations”, Oberwolfach, Germany (invited talk). |
|
[29]
|
F. Bonizzoni. Rational-based MOR methods for parametric-in-frequency Helmholtz problems with adapted snapshots, 14. June 2022 at the ESI Thematic Programme “Computational Uncertainty Quantification: Mathematical Foundations, Methodology & Data", Universität Wien (invited talk). |
|
[28]
|
D. Peterseim. Super-localized numerical homogenization and its links to variational multiscale and isogeometric analysis, 7. June 2022 at the 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Oslo (invited talk). |
|
[27]
|
F. Bonizzoni. H1-conforming finite element cochain complexes on Cartesian meshes, 7. June 2022 at the 8th European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS), Oslo, Norway. |
|
[26]
|
D. Peterseim. The localization problem in numerical homogenization, 23. May 2022 at Asymptotics, Operators, and Functionals Seminar, University of Bath (invited talk, online). |
|
[25]
|
D. Peterseim. Compression of partial differential operators by numerical homogenization, 12. May 2022 at Numerical methods for Compression and Learning, Gran Sasso Science Institute. |
|
[24]
|
F. Bonizzoni. Interplay between Isogeometric and Stochastic collocation for Uncertainty Quantification of timber beams, 14. April 2022 at the SIAM conference on Uncertainty Quantification, Atlanta, Georgia, USA. |
|
[23]
|
F. Bonizzoni. Rational-based MOR methods for parametric-in-frequency Helmholtz problems with adapted snapshots, 15. February 2022 at the Conference on Mathematics of Wave Phenomena, Karlsruhe Institute of Technology, Germany. |
|
[22]
|
D. Peterseim. The localization problem in numerical homogenization, 13. January 2022 at Forschungsseminar Numerische Mathematik, Humboldt-Universität zu Berlin (invited talk, online). |
|
[21]
|
F. Bonizzoni. Model Order Reduction Methods for Time-Harmonic Wave Problems, 1. December 2021 at IWR Kolloquium, Romberg Inaugural Lecture, IWR Heidelberg. |
|
[20]
|
D. Peterseim. On the localization problem in numerical homogenization, 25. November 2021 at Wilhelm Killing Kolloquium, Universität Münster (invited talk). |
|
[19]
|
D. Peterseim. Energy-adaptive Riemannian Optimization on the Stiefel Manifold, 3. November 2021 at Computational and Applied Mathematics (CAM) seminar, Chalmers University of Technology and University of Gothenburg (invited talk, hybrid). |
|
[18]
|
D. Peterseim. Energy-adaptive Riemannian optimization on the Stiefel manifold, 29. September - 1. October 2021 at Numerical Analysis Workshop, Universität Bielefeld (invited talk). |
|
[17]
|
D. Peterseim. Super-localization of elliptic multiscale problems, 22. Septermber 2021 at Second French-German Workshop on Multiscale Problems, Paris. |
|
[16]
|
D. Peterseim. Riemannian gradient flows for nonlinear eigenvector problems, 17.-18. September 2021 at FORTH Heraklion, Crete. |
|
[15]
|
F. Bonizzoni. Rational-based Model Order Reduction methods for parametric Helmholtz problems, 15. September 2021 at the workshop “Scattering by random heterogeneous media”, University of Augsburg, Germany. |
|
[14]
|
F. Bonizzoni. Shape optimization for a noise reduction problem by non-intrusive parametric reduced modeling, 10. September 2021 at the 18th European Finite Element Fair 2021, Inria Paris, France. |
|
[13]
|
F. Bonizzoni. Shape optimization for a noise reduction problem by non-intrusive parametric reduced modeling, 01. September 2021 at SIMAI 2020+2021, Parma, Italy. |
|
[12]
|
F. Bonizzoni. Analytical derivation and sparse approximation of the recursive first moment equations for the Lognormal Darcy problem, 14. July 2021 at ICOSAHOM 2020/2021, Vienna, Austria (online). |
|
[11]
|
D. Peterseim. Super-localization of elliptic multiscale problems, 12. July 2021 at workshop about new trends in numerical multiscale methods and beyond, Institut Mittag-Leffler, Stockholm, Sweden (invited talk, online). |
|
[10]
|
F. Bonizzoni. Shape optimization for a noise reduction problem by non-intrusive parametric reduced modeling, 08. July 2021 at the 6th ECCOMAS Young Investigators Conference, Valencia, Spain (online). |
|
[9]
|
M. Hauck. Multiresolution Localized Orthogonal Decomposition for Helmholtz problems, 25. March 2021 at Sion Young Academics Workshop 2021 (online). |
|
[8]
|
F. Bonizzoni. A reduced order model for the acoustic scattering of an airfoil, 18. March 2021 at the 2021 Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM) (online). |
|
[7]
|
D. Peterseim. Introduction to numerical homogenization of PDEs with arbitrary rough coefficients, 16. March 2021 at the 2021 Annual Meeting of the International Association of Applied Mathematics and Mechanics (GAMM) (online). |
|
[6]
|
D. Peterseim. A priori error analysis of a numerical stochastic homogenization method, 01. March 2021 at Scaling Cascades in Complex Systems 2021, FU Berlin (online). |
|
[5]
|
D. Peterseim. Three thematic lectures on numerical homogenization, 15.-17. February 2021 at ICTS MATHLEC 2021 (invited lecture series, online). |
|
[4]
|
D. Peterseim. Numerical methods for the nonlinear Schrödinger eigenvalue problem, 10. December 2020 at Analysis-Seminar Augsburg-Munich (invited talk, online). |
|
[3]
|
D. Peterseim. Localized Eigenstates by Domain Decomposition, 8. December 2020 at 26th International Domain Decomposition Conference, Chinese University of Hong Kong (online). |
|
[2]
|
D. Peterseim. Nonlinear eigenvector problems and the simulation of Bose-Einstein condensates, 4. December 2020 at Mathematical Colloquium, RWTH Aachen University (invited talk, online). |
|
[1]
|
M. Hauck. Enriched Galerkin - Subcell enrichment and Application to the shallow water equations, 12. October 2020 at MoST 2020. |
Publications
Submitted articles:
|
[50]
|
D. Peterseim, J.-F. Pietschmann, J. Püschel, K. Ruess.Neural Network Acceleration of Iterative Methods for Nonlinear Schrödinger Eigenvalue Problems. ArXiv e-prints, 2025. [ arXiv] |
|
[49]
|
Y. Liang and N. T. Tran. A hybrid high-order method for the biharmonic problem. ArXiv e-prints, 2025. [ arXiv] |
|
[48]
|
D. Peterseim, J. Püschel, T. Stykel. Energy-Adaptive Riemannian Conjugate Gradient Method for Density Functional Theory. ArXiv e-prints, 2025. [ arXiv] |
|
[47]
|
D. Gallistl, N. T. Tran. Minimal residual discretization of a class of fully nonlinear elliptic PDE. ArXiv e-prints, 2024. [ arXiv] |
|
[46]
|
N. T. Tran. Lower eigenvalue bounds with hybrid high-order methods. ArXiv e-prints, 2024. [ arXiv] |
|
[45]
|
C. Carstensen, N. T. Tran. Locking-free hybrid high-order method for linear elasticity. ArXiv e-prints, 2024. [ arXiv] |
|
[44]
|
M. Deiml, D. Peterseim. Nonlinear quantum computing by amplified encodings. ArXiv e-prints, 2024. [ arXiv] |
|
[43]
|
J. C. Garay, H. Mohr, D. Peterseim, C. Zimmer. Hierarchical Super-Localized Orthogonal Decomposition Method. ArXiv e-prints, 2024. [ arXiv] |
|
[42]
|
M. Hauck, Y. Liang, D. Peterseim. Positivity preserving finite element method for the Gross-Pitaevskii ground state: discrete uniqueness and global convergence. ArXiv e-prints, 2024. [ arXiv] |
Refereed articles:
|
[41]
|
M. Deiml, D. Peterseim. Quantum Realization of the Finite Element Method. Math. Comput, 2025. |
|
[40]
|
C. Belponer, J. C. Garay, P. Munch, D. Peterseim. Super-Localized Orthogonal Decomposition Method for Heterogeneous Linear Elasticity. Comput. Methods Appl. Math., 25:561-579, 2025. |
|
[39]
|
R. Altmann, M. Hermann, D. Peterseim, T. Stykel, Riemannian optimisation methods for ground states of multicomponent Bose-Einstein condensates. IMA J. Numer. Anal., draft046, 2025. |
|
[38]
|
N. T. Tran. Finite element approximation for uniformly elliptic linear PDE of second order in nondivergence form. Math. Comput., 94.353: 1043-1064, 2025. |
|
[37]
|
S. C. Hawkins, L. G. Bennetts, M. A. Nethercote, M. A. Peter, D. Peterseim, H. J. Putley, B. Verfürth. Metamaterial applications of Tmatsolver, an easy-to-use software for simulating multiple wave scattering in two dimensions. Proceedings of the Royal Society A, 480:20230934, 2024. [ OPUS Augsburg | DOI] |
|
[36]
|
N.T. Tran. Discrete weak duality of hybrid high-order methods for convex minimization problems. SIAM J. Numer. Anal. 62, 1492-1514, 2024. |
|
[35]
|
C. Carstensen, B. Gräßle, N. T. Tran, Adaptive hybrid high-order method for guaranteed lower eigenvalue bounds. Numer. Math. 156: 813-851, 2024. |
|
[34]
|
D. Gallistl, N. T. Tran, Stability and guaranteed error control of approximations to the Monge–Ampère equation. Numer. Math. 156.1: 107-131, 2024. |
|
[33]
|
D. Gallistl, M. Hauck, Y. Liang, D. Peterseim. Mixed finite elements for the Gross-Pitaevskii eigenvalue problem: a priori error analysis and guaranteed lower energy bound. IMA J. Numer. Anal., 2024. [ arXiv | DOI] |
|
[32]
|
M. Hauck, H. Mohr, D. Peterseim. A simple collocation-type approach to numerical stochastic homogenization. Multiscale Model. Simul. 23.1: 374-396, 2025. |
|
[31]
|
R. Altmann, D. Peterseim, T. Stykel. Riemannian Newton methods for energy minimization problems of Kohn-Sham type. J. Sci. Comput. 101.1: 6, 2024. |
|
[30]
|
F. Bonizzoni, K. Hu, G. Kanschat, D. Sap. Discrete tensor product BGG sequences: splines and finite elements. Math. Comput. 94.352: 517-549, 2025. [ arXiv | DOI] |
|
[29]
|
M. Alghamdi, D. Boffi and F. Bonizzoni. A greedy MOR method for the tracking of eigensolutions to parametric elliptic PDEs. J. Comput. Appl. Math. 457: 116270, 2025. |
|
[28]
|
P. Freese, M. Hauck and D. Peterseim. Super-localized Orthogonal Decomposition for high-frequency Helmholtz problems. Siam J. Sci. Comput., 46: 2377-2397, 2024. |
|
[27]
|
F. Bonizzoni, P. Freese and D. Peterseim. Super-localized orthogonal decomposition for convection-dominated diffusion problems. BIT Numer. Math., 64: 33, 2024. [ arXiv | DOI] |
|
[26]
|
M. Hauck and A.Målqvist. Super-localization of spatial network models. Numer. Math., 156: 901-926, 2024. [ arXiv | DOI] |
|
[25]
|
D. Peterseim, J. Wärnegård, C. Zimmer. Super-localised wave function approximation of Bose-Einstein condensates. J. Comput. Phys., 510: 113097, 2024. [ arXiv | DOI] |
|
[24]
|
F. Bonizzoni, M. Hauck, and D. Peterseim. A reduced basis super-localized orthogonal decomposition for reaction-convection-diffusion problems. J. Comput. Phys., 499: 112698, 2024. |
|
[23]
|
P. Freese, M. Hauck, T. Keil and D. Peterseim. A Super-Localized Generalized Finite Element Method. Numer. Math., 156: 205-235, 2024. |
|
[22]
|
P. Freese, D. Gallistl, D. Peterseim, T. Sprekeler. Computational multiscale methods for nondivergence-form elliptic partial differential equations. J. Comput. Methods Appl. Math., 2023. [ arXiv | DOI] |
|
[21]
|
Z. Dong, M. Hauck and R. Maier. An improved high-order method for elliptic multiscale problems. SIAM J. Numer. Anal., 61(4): 1918-1937, 2023. |
|
[20]
|
G. Balduzzi, F. Bonizzoni, L. Tamellini. Uncertainty quantification in timber-like beams using sparse grids: theory and examples with off-the-shelf software utilization. Constr. Build. Mater., 406: 132730, 2023. |
|
[19]
|
F. Bonizzoni, D. Pradovera and M. Ruggeri. Rational-approximation-based model order reduction of Helmholtz frequency response problems with adaptive finite element snapshots. Math. Eng., 5(4): 1-38, 2023. |
|
[18]
|
F. B onizzoni, G. Kanschat. A Tensor-Product Finite Element Cochain Complex with Arbitrary Continuity. eccomas2022, 2022. [ DOI] |
|
[17]
|
P. Freese. The Heterogeneous Multiscale Method for dispersive Maxwell systems. Multiscale Model. Simul., 20(2): 769-797, 2022. [ DOI] |
|
[16]
|
R. Altmann, D. Peterseim and T. Stykel. Energy-adaptive Riemannian optimization on the Stiefel manifold. ESAIM: M2AN, 56(5): 1629-1653, 2022. |
|
[15]
|
F. Kröpfl, R. Maier and D. Peterseim. Operator compression with deep neural networks. Adv. Cont. Discr. Mod., 29, 2022. |
|
[14] |
M. Hauck and D. Peterseim. Super-localization of elliptic multiscale problems. Math. Comput., 92: 981-1003, 2023. |
|
[13]
|
M. Hauck and D. Peterseim. Multi-resolution Localized Orthogonal Decomposition for Helmholtz problems. Multiscale Model. Simul., 20(2): 657-684, 2022. [ DOI] |
|
[12]
|
R. Altmann, P. Henning and D. Peterseim. Localization and delocalization of ground states of Bose-Einstein condensates under disorder. SIAM J. Appl. Math., 82, 330-358, 2022. [ arXiv | DOI] |
|
[11]
|
R. Altmann, P. Henning and D. Peterseim. The J-method for the Gross-Pitaevskii eigenvalue problem. Numer. Math., 148(3): 575-610, 2021. [ arXiv | DOI] |
|
[10]
|
R. Altmann, P. Henning and D. Peterseim. Numerical homogenization beyond scale separation. Acta Numerica, pp. 1-86, 2021. [ DOI] |
|
[9]
|
J. Fischer, D. Gallistl and D. Peterseim. A priori error analysis of a numerical stochastic homogenization method. SIAM J. Numer. Anal., 59(2): 660-674, 2021. [ arXiv | DOI] |
Monograph:
|
[8]
|
A. Målqvist and D. Peterseim. Numerical homogenization by localized orthogonal decomposition. SIAM Spotlights 5, ISBN: 978-1-611976-44-1, 2020. [ SIAM] |
Dissertations:
|
[7]
|
H. Mohr. Super-Localized Orthogonal Decomposition for deterministic and stochastic homogenization problems. Dissertation, University of Augsburg, Faculty of Mathematics, Natural Sciences, and Technology, Augsburg, Germany, 2025 (submitted). |
|
[6]
|
F. Kröpfl. Deep-learning-based numerical homogenization of heterogeneous media. Dissertation, University of Augsburg, Faculty of Mathematics, Natural Sciences, and Technology, Augsburg, Germany, 2024. [ OPUS Augsburg] |
|
[5]
|
M. Hauck. Numerical homogenization: multi-resolution and super-localization approaches. Dissertation, University of Augsburg, Faculty of Mathematics, Natural Sciences, and Technology, Augsburg, Germany, 2023. |
Preliminary Work
|
[4]
|
M. Feischl and D. Peterseim. Sparse compression of expected solution operators. SIAM J. Numer. Anal., 58(6):3144-3164, 2020. |
|
[3]
|
P. Henning and D. Peterseim. Sobolev gradient flow for the Gross-Pitaevskii eigenvalue problem: global convergence and computational efficiency. SIAM J. Numer. Anal., 58(3):1744–1772, 2020. [ arXiv | DOI] |
|
[2]
|
R. Altmann, P. Henning, and D. Peterseim. Quantitative Anderson localization of Schrödinger eigenstates under disorder potentials. M3AS Math. Models Methods Appl. Sci., 30(5):917-955, 2020. |
|
[1]
|
D. Peterseim and B. Verfürth. Computational high frequency scattering from high contrast heterogeneous media. Math. Comp., 89:2649-2674, 2020. [ arXiv | DOI] |
